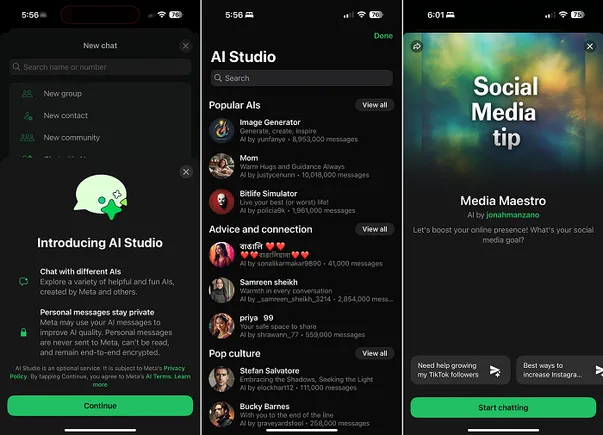
A bit of a technical explanation on how Bitcoin mining works
When searching for a block, the miner hashes the transactions along with other block data and modifies the nonce and block timestamp to generate different hash outputs. The hashing function used is SHA-256, which produces a 256-bit hash. The network difficulty (currently 119T) determines how small the hash must be in order to successfully mine a block. The formula is super simple: 2²⁵⁶ (SHA-256 produces a 256-bit output) ÷ Network difficulty (119T) -> 1,190,000,000,000 Conclusion: The higher the network difficulty, the smaller the block hash must be to be considered valid. This explains why the number of leading zeros in the block hash increases as difficulty rises. For example, in binary: 0001 is smaller than 0100. The total number of possible SHA-256 hashes is 2²⁵⁶, which is such a huge number that finding a hash smaller than 2²⁵⁶ / 119T is practically impossible. submitted by /u/neo69654 [link] [comments]
When searching for a block, the miner hashes the transactions along with other block data and modifies the nonce and block timestamp to generate different hash outputs.
The hashing function used is SHA-256, which produces a 256-bit hash.
The network difficulty (currently 119T) determines how small the hash must be in order to successfully mine a block.
The formula is super simple:
2²⁵⁶ (SHA-256 produces a 256-bit output) ÷ Network difficulty (119T) -> 1,190,000,000,000
Conclusion:
- The higher the network difficulty, the smaller the block hash must be to be considered valid.
- This explains why the number of leading zeros in the block hash increases as difficulty rises.
- For example, in binary:
- 0001 is smaller than 0100.
The total number of possible SHA-256 hashes is 2²⁵⁶, which is such a huge number that finding a hash smaller than 2²⁵⁶ / 119T is practically impossible.
[link] [comments]


![How to Find Low-Competition Keywords with Semrush [Super Easy]](https://static.semrush.com/blog/uploads/media/73/62/7362f16fb9e460b6d58ccc09b4a048b6/how-to-find-low-competition-keywords-sm.png)

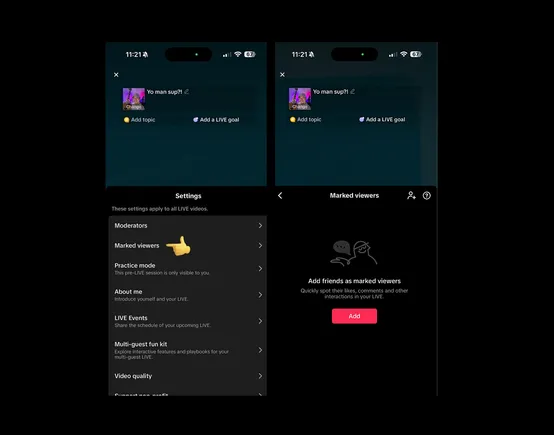






































































































































































.jpg)
%20Abstract%20Background%20112024%20SOURCE%20Amazon.jpg)